作者：Jon Gulson，Bitcoin Magazine；編譯：松雪，金色財經

“我認爲經濟學有點像會計 —— 你知道的，它並不涉及任何道德。你可以研究福利經濟學，嘗試考慮一些人類價值觀，或者你可以研究各種變體。” —— 約翰·F·納什 Jr.，斯克蘭頓大學，2011年11月。

這段引自約翰·福布斯·納什·Jr.的語錄——來自他在“理想貨幣和儲蓄與節儉動機”上的一次演講，此次演講距離他第一篇博弈論論文《討價還價問題》（1950年）發表已有61年。

《討價還價問題》之所以重要，是因爲它被認爲是社會科學中首次引入公理方法的例子之一。納什將《討價還價問題》作爲一個對古典經濟問題的新處理 —— 將其視爲一個非零和、兩人博弈，在這個博弈中他做出了一些一般性假設和“某些理想化”，以便爲博弈找到值。

從《討價還價問題》到納什後來關於理想貨幣的研究的基因譜系被確立，而在《討價還價問題》中，納什對貨幣的效用進行了評論：

“當討價還價者有一個共同的交換媒介時，問題可能呈現出特別簡單的形式。在許多情況下，商品的貨幣等價物將作爲一個令人滿意的近似效用函數。” 約翰·F·納什 Jr.，《討價還價問題》（1950）。

納什的討價還價探討在金融交易或合同中，如何在參與者之間公平地分割1美元，每一方都有一系列的興趣和偏好，並且必須達成協議，否則雙方都將一無所得。爲納什交易引入的公理隨後定義了一個唯一的解決方案。

納什均衡與納什討價還價

在《The Essential John Nash》（2007）中，哈羅德·庫恩描述了納什隨後的《Non-Cooperative Games》（1950）論文，以及後來被稱爲Nash均衡的理論，他稱之爲對Brouwer不動點定理的“笨拙，但完全獨創的應用”。然而，正是納什的均衡概念通過經濟科學諾貝爾獎賦予他公衆關注。後來，納什的生平被改編成了好萊塢電影《美麗心靈》。

在《Non-Cooperative Games》中，納什的理論基於“聯盟的缺席，即假設每個參與者都是獨立行動的，沒有與任何其他人的合作或溝通”。在亞當·柯蒂斯（Adam Curtis）的電視紀錄片《陷阱》（2007）中，納什將他的均衡理論描述爲社會調整：

“……所使用的這種均衡是，我所做的完全與你所做的相適應，而你所做的或任何其他人所做的也完全適應我所做的或所有其他人所做的。他們正在尋求獨立的優化，就像撲克牌玩家一樣。” 約翰·F·納什 Jr.，《陷阱》（2007, 亞當·柯蒂斯），《F*ck You, Buddy》。

納什均衡和納什討價還價的區別在於，公理討價還價（或達成納什討價還價）不假定均衡。相反，它陳述了解決方案的期望性質。納什討價還價被認爲是合作博弈論，因爲它具有非零和的特性和合同的存在。納什在《Two-Person Cooperative Games》（1953）中擴展了對《討價還價問題》的公理處理，在這一過程中引入了一種威脅方法，其中有一名裁判來執行合同 —— 在這個過程中，將“策略”視爲不具有特殊品質，而更關注確定博弈的形式表示。

理想貨幣和漸近理想貨幣

在世紀之交，約翰·納什开始撰寫並講授一個不斷演變的名爲理想貨幣的論文。隨着多年的發展，這個理論經歷了不同的迭代，但納什定義它爲內在免受通貨膨脹或通貨膨脹性墮落的貨幣。納什對經濟學家或個人凱恩斯並不是那么批判，而是對所謂的凱恩斯主義心理學的批評；納什認爲這是一種持續通貨膨脹和貨幣貶值的權謀計劃。納什認爲，如果中央銀行要以通貨膨脹爲目標，他們應該將“所謂的通貨膨脹”定爲零率：

“真正令人尊敬的是，通貨膨脹不應該有任意或反復無常的模式，但如何定義一種合適和理想的貨幣價值穩定形式呢？” 約翰·F·納什 Jr.，《理想貨幣和漸近理想貨幣》（2010）。

在《理想貨幣》中，納什回到了他在初期博弈論中首次建立的公理方法。因此，理想貨幣對凱恩斯宏觀經濟學提出了批評：

“因此，我認爲凱恩斯派的宏觀經濟學可與使用不足的公理集進行的數學領域的科學研究相媲美。” 約翰·F·納什 Jr.，《理想貨幣和漸近理想貨幣》（2008）。

納什定義了缺失的公理：

“缺失的公理就是一個被接受的公理，即由中央當局投放市場的貨幣應該被處理得以在很長時間內保持穩定的價值。” 約翰·F·納什 Jr.，《理想貨幣和漸近理想貨幣》（2008）。

在2002年的《理想貨幣》南方雜志版本中，納什意識到理想貨幣不能完全免受通貨膨脹（或過於“良好”），因爲它將在流通中遇到問題，並可能被希望安全存放財富的一方所利用。納什隨後引入了一個穩定而恆定的通貨膨脹率（或漸近线），該率可以被添加到借貸合同中。

確實，納什在合作博弈和微觀經濟背景下描述了理想貨幣的目的：

“一個我們在初次思考理想貨幣時沒有考慮到，後來才意識到的概念是，在一個經濟社會中使用的貨幣的比較質量對於合同的精確性至關重要，作爲未來合同履行的質量指標。” 約翰·F·納什 Jr.，《理想貨幣和漸近理想貨幣》（2008）。

比特幣作爲一種公理設計

如果納什對經濟學的看法是它缺乏任何直接的道德觀念 —— 價值觀、假設、公理、變體或理想化可以被引入以確定一個非零和或確定的博弈，爲所有參與者提供福祉 —— 那么值得考慮的是，這些公理是否存在於比特幣系統中，鑑於納什與中本聰一起都對中央管理貨幣的任意（或不確定）性質提出了批評。

帕累托效率

在比特幣的累積供應密度和分布方面，帕累托效率的存在可能是最具示範性的納什討價還價公理（見圖示）：大多數比特幣在比特幣歷史的早期被挖出（大致地遵循帕累托80/20冪律）。

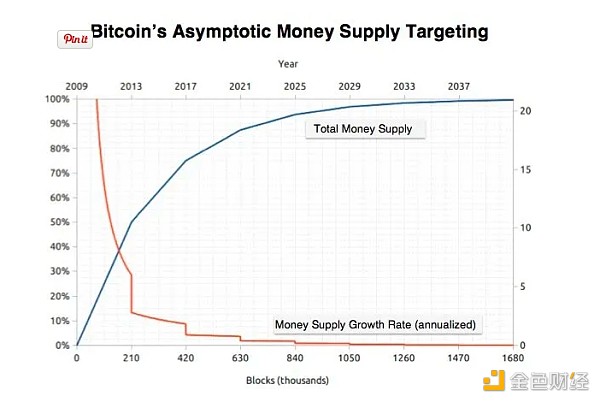
1.尺度不變性

尺度不變性通過難度調整機制而存在，該機制使比特幣供應“穩定而恆定”（納什和中本聰都使用過這個詞）。無論比特幣變得多么受歡迎或不受歡迎，尺度不變性應該意味着參與者可以形成有關比特幣價值的現實期望，而其基本偏好在這方面不應該發生變化。比特幣的內部可分割性也意味着在較短或即時時間範圍內，一個幣的表達價值（無論是美元還是其他貨幣）不應該有關系 —— 就像室溫可以用攝氏度或華氏度表示而不影響實際溫度一樣。這些差異只在較長期或跨時間的交易中才會變得明顯。

調整機制還使比特幣的總供應量保持在2100萬以下，這是由於系統數據結構的副作用，因此這樣設定。

2.對稱

納什的對稱性公理存在於比特幣網絡的匿名和去中心化中，通過在參與核心或主要網絡時無需證明第一人稱身份，實現了匿名（納什在《討價還價問題》中引入的一種說法）。這意味着沒有一個中心化或受信任的主體負責鑄造比特幣，用納什的話說是一個“大赦者”。與納什討價還價相關，如果兩個玩家有相同的效用函數，因此是不可區分的，那么它們應該得到相同的數量。阿爾文·羅斯（1977年）總結爲玩家的標籤無關緊要：“如果切換玩家的標籤不會改變討價還價問題，那么它就不應該改變解決方案。”

3.不相關替代方案的獨立性 (IIA)

最後，有納什最具爭議的討價還價公理：無關替代品的獨立性。簡單來說，這意味着在兩名玩家之間的選舉中添加第三方（或非獲勝候選人）不應該改變選舉的結果（第三方變得無關緊要）。如果點對點是指一個兩名玩家的遊戲，比特幣網絡充當第三方仲裁者或裁判員對“遊戲”進行操作，該軟件設計爲一組價值觀或公理，那么在比特幣的工作證明中可能存在無關替代品的獨立性。這涉及到社會群體偏好的背景：工作證明表示它解決了在多數決策中確定代表的問題，並且納什的討價還價公理（無論是在《討價還價問題》還是《兩人合作博弈》中）明確解決了決定性遊戲中的正式代表問題。

合作特點及效益

一般來說，合作博弈需要具備三個條件：

1.減少參與者，即兩名玩家。

2.合同，參與者能夠就合理的聯合行動計劃達成一致，可由法院等外部機構強制執行。

3.參與者能夠在可信信息的基礎上進行交流和協作，並能夠完全訪問遊戲的結構（例如比特幣區塊鏈）。

在非零和遊戲和貨幣偏好方面，約翰·納什思考了貨幣如何通過“潤滑”促進可轉讓的效用，並做出了以下觀察：

“在博弈論中，通常有‘收益’的概念，如果遊戲不僅僅是贏或輸（或贏、輸或平局的遊戲）。遊戲可能涉及到同時進行的所有行動，以便用於定義收益的效用度量可以在相關時刻採用任何具有良好可分性和可測性特性的實際貨幣。” 約翰·F·納什（John F. Nash Jr.），《理想貨幣與儲蓄和節儉的動機》（2011）。

合作的好處包括減少對調解或糾紛解決的需求，因爲合同和協議變得更加可信任；在貿易中減少邊境摩擦；非零和結果（雙贏的討價還價或福利經濟學）；更直觀、非正式的決策制定；以及形成聯盟的可能性，這正是約翰·納什最終定義的世界帝國背景。後者使得解決諸如零淨排放（或任何其他需要多邊協調的問題）的困難問題更加現實。納什將他的理想貨幣提議比作老式的主權貨幣：

“任何版本的理想貨幣（本質上不受通貨膨脹影響的貨幣）都必然類似於提供用於交易的實用媒體的古典‘君主’或‘領主’。” 約翰·F·納什（John F. Nash Jr.），《理想貨幣與儲蓄和節儉的動機》（2011）。

2011年，納什還思考了一個“合同籤署”的“遊戲”，仿佛理想貨幣就是這份合同：

“就好像在合同籤署者的遊戲中還有另一個玩家，而這個玩家就是君主，他以貨幣的形式提供了合同的表達方式。” 約翰·F·納什（John F. Nash Jr.），《理想貨幣與儲蓄和節儉的動機》（2011）。