比特幣生態擴容方案巡禮(2): BitVM——蝕刻的藝術
2023-12-29 15:19 MetaTrust Labs
作者:Simon shieh,來源:MetaTrust Labs
前言回顧
上一篇《比特幣生態擴容方案巡禮(1):銘文何去何從》中,我們討論了熱門的銘文生態的技術原理和可能存在的安全問題,並且提到了用遞歸銘文來實現智能合約的可能性。但是因爲Luke對Taproot腳本的限制,遞歸銘文似乎有了一些障礙,那在比特幣網絡上實現智能合約有沒有其他的可能性呢?
區塊鏈开發商ZeroSync的聯合創始人Robin Linus,在2023年10月9日發表了一篇名爲“BitVM:在比特幣上進行所有運算(BitVM:Compute Anything on Bitcoin)”的論文,其中提出了一個計劃,旨在將智能合約引入比特幣區塊鏈。

該論文提出了一個非常有趣的思路,可以用taproot完成幾乎所有的任意計算,並使用這些計算來驗證在比特幣鏈下發生的事情。其中的訣竅是,將所有的邏輯都放在鏈下,並在其他人斷言了不誠實的結果時,在鏈上用少數幾步計算來挑战這些結果。
換句話說,就是將一個Verifier的邏輯放在比特幣網絡中,利用比特幣的強共識安全,成爲任何圖靈完備運算層的可信第三方,再用Optimistic Rollups 的原理,來實現鏈外計算結果的驗證。
那么怎么實現將一段Verifier的邏輯放在比特幣網絡中呢?爲了和上一節的“銘刻”相呼應,我愿稱之爲在比特幣網絡上進行電路“蝕刻”的技術。
邏輯門電路
在你的電腦或手機內部,電流通過傳遞一系列的1和0來實現計算機的所有功能。這是通過數以百萬計的微小組件——邏輯門(logic gates)——來實現的。這些邏輯門是構成計算機芯片的基本元素。
每個邏輯門都會接收一個或兩個“比特(bit)”的信息,每個比特要么是1,要么是0。然後,邏輯門根據設定的規則執行一個簡單的邏輯運算,如“與(AND)”、“或(OR)”或“非(NOT)”等操作。這些運算產生的結果同樣是一個比特,也是1或0。完成運算後,這個結果又被傳遞到下一個邏輯門。
這種基於簡單邏輯運算的系統產生了啓示:即使是最復雜的計算和功能,也都可以通過組合大量簡單的邏輯運算來實現。這種邏輯門的組合和協作是現代計算機和電子設備能夠執行復雜任務的基礎。通過這些基本的邏輯操作,電腦能夠處理復雜的算術運算、數據存儲、圖像渲染等功能。
下圖是一個非常特殊的邏輯門,叫做“與非門”(NAND gate),它可以構造任意類型邏輯門電路,當然,它不可能有其它專用類型的門那么高效,但還是能做到的。BitVM的邏輯門電路就由與非門組成。
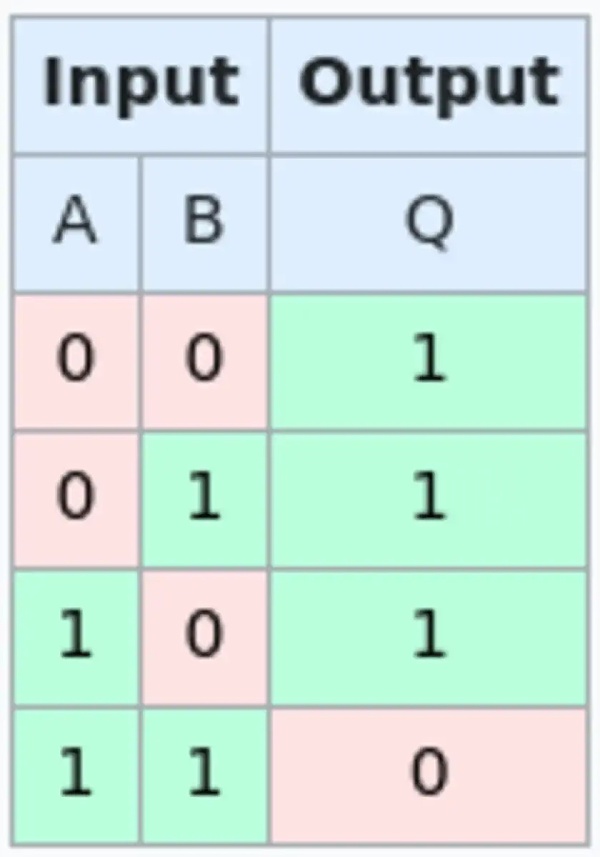
比特幣上如何蝕刻與非門
在現有的比特幣腳本上構造與非門(NAND gate)可以通過結合哈希鎖和兩個可能不太爲人所熟知的操作碼:OP_BOOLAND和OP_NOT來實現。
首先,哈希鎖可以用來創建一個分支腳本,這個腳本可以通過兩種方式中的一種來花費:要么滿足哈希鎖,要么滿足哈希鎖B。這樣,路徑A將1輸出到堆棧,而路徑B將0輸出到堆棧。
通過滿足特定哈希鎖,你可以"解鎖"一個比特,這個比特作爲我們要構造的NAND門的輸入之一。由於你只能滿足其中一個路徑的要求,所以這種方法只允許用戶一次提交一個比特。
與非門的邏輯是接收兩個比特作爲輸入,輸出一個比特。如果兩個輸入比特都是1,則輸出0;如果輸入是其他組合,則輸出1。使用兩個哈希鎖技巧,可以提交這兩個輸入,並驗證輸出是否正確,這就是OP_BOOLAND和OP_NOT的用途所在。
OP_BOOLAND的操作與與非門相反:如果兩個輸入都是1,則輸出1;任何其他輸入組合都會產生0。OP_NOT則輸出與輸入相反的值。因此,通過結合使用這兩個操作碼,可以在腳本堆棧中取兩個輸入並進行反和操作。最後,可以使用OP_EQUALVERIFY以及哈希鎖技巧來驗證斷言的輸出。如果堆棧中實際的與非操作結果與用戶斷言的輸出不一致,腳本就無法通過驗證。
這樣,就在比特幣腳本中“蝕刻”了與非門電路,實際上是通過比特幣腳本來強制執行虛擬的與非門操作。
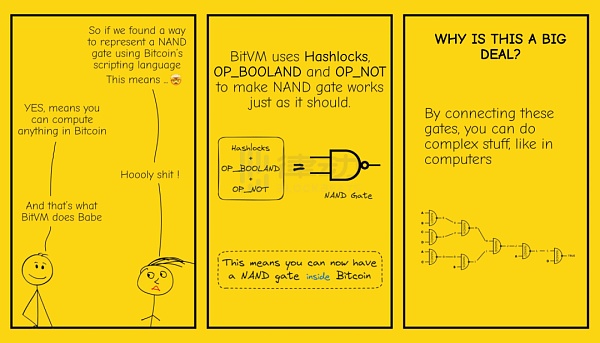
如何蝕刻大規模電路
雖然這個利用Taproot腳本實現電路蝕刻的想法很酷,但是別說像PC那種超大規模電路了,就是要實現任意一組計算,都需要成千上萬的與非門電路,那在比特幣有限的Taproot腳本空間裏,如何覆蓋復雜計算呢?
BitVM提出了Taproot腳本樹(Taproot Tree)的方法。爲了在比特幣腳本中實現復雜的計算過程,人們可以通過串聯邏輯門來構建計算電路。在這個方案中,哈希鎖被用來綁定各個門,從而實現順序執行的邏輯操作。具體來說,如果一個門的腳本根據不同的哈希原像(哈希明文值)輸入產生不同的輸出結果C1或C2,那么下一個門會使用與之相匹配的哈希鎖值作爲其輸入。
這種方法可以實現一種懲罰機制,即如果試圖謊報前一個門的結果,就只能揭曉另一個哈希鎖的原像。這種機制可以用於兩個用戶之間的交互式計算,其中他們預先同意參與特定的計算任務,然後將計算過程分解成只由與非門組成的電路。他們需要爲電路中的每個門選擇合適的哈希鎖,並將其編碼進鎖定UTXO的腳本樹中。
然後通過多個地址組成一個Taproot地址矩陣,再通過Taproot Tree的方式將邏輯電路蝕刻到一系列樹狀結構相連的UTXO交易的Taproot腳本中,最終形成一個可以處理一定計算任務的“類合約”邏輯電路。
欺詐挑战
欺詐挑战是OP(Optimism Rollup)技術的核心(雖然至今都沒有真的實現~),思想是在一個batch的交易被批量提交之前,挑战者對認爲有錯的交易發起欺詐挑战(質押對賭),主網上的Verifier合約會根據狀態根在執行後的變化來判斷提交者是否作惡,然後分配雙方質押的資產。
而在bitVM中,腳本樹被設計成兩個電路,除了允許證明者提交到一個電路之外,還需要挑战者能夠挑战證明者的聲明。這可以通過預籤名一系列的交易來實現。這些預籤名交易通過「挑战 ->應答 ->挑战 ->…」的方式連接。如果某一方停止一段時間後,另外一方就會贏得挑战並回收雙方的存款。
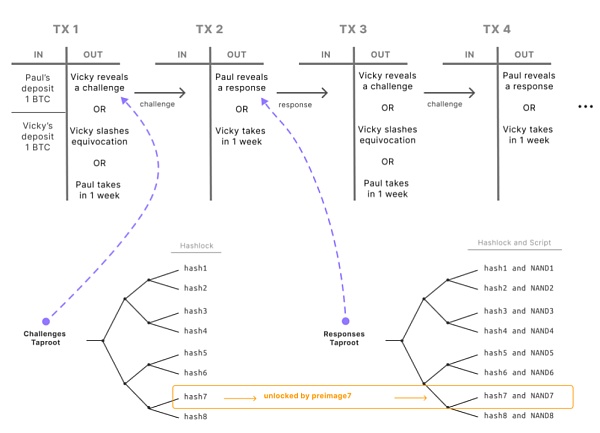
上圖展示了一系列預先籤名的交易:
• 挑战:Vicky (挑战者 / 驗證者)在腳本路徑中釋放一個原像(這些原像只有挑战者知道),用作對證明的挑战;
• 應答:Paul (證明者)執行對應的邏輯門,將資金發回初始的腳本中;
在幾輪的查詢後可以迅速駁斥任何一個不一致的聲明。如果證明者停止在鏈下與挑战者合作,挑战者就會強制證明者在鏈上合作:挑战者每解鎖一個哈希鎖,使得證明者的 UTXO 中的每個 NAND 門對應的 Taproot 葉子節點只有在證明者知道挑战者持有的一個原像時才可以被花費。證明者可以通過揭示其輸入和輸出來證明給定的 Taproot 葉子節點執行正確。其前提是挑战者通過揭露對應 Tapleaf 的哈希的原像來解鎖它,通過二分查找的方式,挑战者可以在經過有限輪(O(logn))的挑战和應答後鎖定證明者的錯誤。
整個過程涉及到多輪交互,以確保合約能夠正確結算。挑战者可以不斷挑战證明者,直到證明者證實了每個門的正確結果,或者在證明者無法響應挑战的情況下,挑战者可以在特定時間後提取資金。在理想情況下,所有操作都在鏈下進行,雙方協作完成結算,但如果合作破裂,雙方可以通過鏈上的挑战遊戲來確保合約得到正確的解決。
落地障礙與安全性問題
這項提議涉及處理和生成的數據量極其龐大。使用的Taproot腳本樹可能包含數十億個葉子節點,而相關的預先籤名交易的處理時間可能至少需要幾個小時,以確保准確的結算。每個Taproot地址的預設解鎖條件執行都需支付礦工費,因此地址組合越多,成本也越大。
這種方案的一個主要限制在於,它只適用於兩個參與者之間的交互:一個作爲證明者,證明其執行的准確性;另一個作爲驗證者,挑战前者的聲明。雖然未來的研究可能會找到方法讓更多參與者加入,但目前看來還沒有明確的解決方案。
在合作結算的場景中,所有參與者必須在线,這對於協議的實用性和便利性構成了一定的限制。
在安全性方面,主要有以下幾點安全風險:
1、由於成本的限制,必然大量的計算工作要放在鏈下進行,鏈下計算就存在中心化服務的一些常見安全風險。
2、大量數據保存在鏈下,數據可用性和數據安全性也是必須要考慮的風險點
3、對於所蝕刻的電路本身是否存在邏輯漏洞也是一個安全風險點,由於電路的不易讀性,需要付出更多的審計成本或形式化驗證成本。
Metatrust曾經協助Uniswap進行了全面的形式化驗證工作,並在ZK電路審計和形式化驗證方面有非常豐富的經驗,可以爲BitVM生態的安全落地,提供保障。
上兩篇的方案都是今年剛火熱起來的技術方案,下一篇,我們將介紹一個更加古老,更加具備“正統性”的方案,閃電網絡的升級版本——Taproott Assets。
鄭重聲明:本文版權歸原作者所有,轉載文章僅為傳播信息之目的,不構成任何投資建議,如有侵權行為,請第一時間聯絡我們修改或刪除,多謝。
標題:比特幣生態擴容方案巡禮(2): BitVM——蝕刻的藝術
地址:https://www.sgitmedia.com/article/19562.html
相關閱讀:
- IntoTheBlock 聯創:Web3基礎設施正在被過度建造 我們正在盲目行事 2024-12-20
- 國際清算銀行最新提出的央行數字貨幣框架究竟是什么? 2024-12-20
- SOL 質押完整指南:從機制和收益等方面解析 Solana 質押生態 2024-12-20
- 特朗普正式獲得總統職位 BTC儲備競賽即將开啓 2024-12-20
- 預防量子計算威脅實用指南 2024-12-20
- 特朗普兩年時間通過加密貨幣賺了多少錢? 2024-12-20
- Chainalysis:朝鮮黑客從加密平台竊取的錢都幹什么了? 2024-12-20
- 估值45億美元,OpenAI和谷歌大佬聯手創立的AI Agent公司爲何這么牛? 2024-12-20
