TL;DR

• SNARK 的構建流程是什么樣的？
  

  待證明的問題-算術電路-R1CS-多項式

• 爲什么最終要轉換成多項式？

  因爲多項式的特性有效的縮短了驗證時間，實現了簡潔性。

• 是如何實現零知識的？

  簡單來說，就是在推導多項式的過程中，多選取兩個隨機數，以此推導出的多項式能讓驗證者無法從中獲取原多項式的系數，即證明者的祕密輸入，以此實現 ZK。

• 怎么實現非交互？

  在證明开始前，引入了一個第三方，即可信設置，將原本驗證者挑選隨機數的任務交給了可信設置，從而實現驗證者和證明者之間的非交互。

ZK 技術近兩年在 Web3 領域備受關注。從 Rollup 开始，越來越多不同賽道的項目都开始嘗試使用 ZK 技術。在這之中，SNARK 和 STARK 是大家最常聽到的兩個名詞，爲了後期更好地理解ZK技術的應用，本文將從非技術的角度簡化闡述 SNARK 的證明邏輯，然後會以 Scroll 的 zk Rollup 爲例來說明 zk 證明系統的運行。

文章旨在闡述基本邏輯，便於閱讀，會盡量避免術語使用，且不會深入探討數學轉換等細節，如有疏漏，敬請諒解。

2012年1月，加州大學伯克利分校教授 Alessandro Chiesa 與人合作撰寫了 SNARK 的論文，提出了術語 zk-SNARK。

zk-SNARK，全稱 Zero-Knowledge-Succinct Non-Interactive Argument of Knowledge，是使用了 ZK技術的一種證明系統。需要注意的是，SNARK 是一類方案的名稱，有很多不同的組合方法都可以實現 SNARK。

• 零知識（Zero-Knowledge）：只有證明者知道的內容將會被隱藏，除了證明者，其他任何人都無法看到。

• 簡短（Succinct）：生成的證明小，驗證時間快。

• 非交互性（Non-Interactive）：證明者和驗證者之間交互很少，甚至沒有。

• 論證（Argument）：驗證者的驗證只對計算能力受限的證明者有效，因爲擁有超強計算能力的證明者可以僞造證明，也就是說，系統具備計算可靠性。

• 知識（Knowledge）：證明者只有知道一些驗證者不知道的信息才能計算出證明。

zk-SNARK 要解決的是“計算驗證問題”，即驗證者能否在不知道證明者隱私的情況下，高效地驗證計算結果。

下面將以 zk-SNARK 的簡化版構建流程來說明該系統是如何結合零知識達到高效驗證的。

zk-SNARK 的構建

將待證明問題轉化爲多項式

簡單來說，SNARK 的思路是將證明陳述是否成立轉換成證明多項式等式是否成立。

整個轉換過程：待求證的問題➡算術電路➡R1CS➡多項式➡多項式之間的轉換

待求證的問題➡算術電路

要通過計算證明一個問題是否爲真，首先就要將待證明的問題轉化成一個計算問題，而任何計算都可以描述爲一個算術電路。

算術電路通常由常數、“加法門”、“乘法門”組成，通過門的疊加，我們可以構建出復雜的多項式。

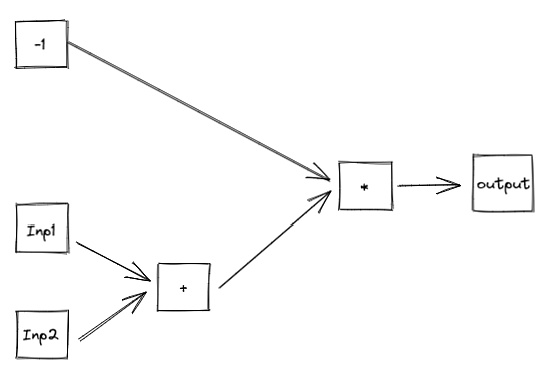
上圖中的算術電路構建的多項式爲：（Inp1+Inp2）*（-1）= Output

現實中的問題要轉爲算術電路極其復雜，我們可以將之簡單理解爲：輸入一些內容，內容經過電路轉化，最終輸出一個結果。即：

基於算術電路的概念，我們構造一個用於生成證明的算術電路，即：

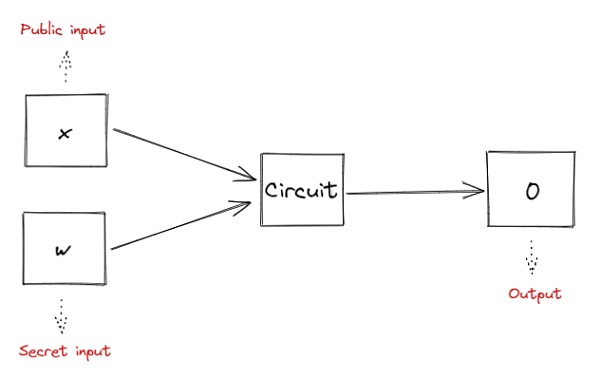
該電路中包含了兩組輸入，公开輸入 x  和祕密輸入w。公开輸入x意味該內容是待證明問題的固定值，驗證者和證明者都知曉，祕密輸入 w 則意味着該內容只有證明者知曉。

我們構建的算術電路爲 C( x, w ) = 0，即通過電路輸入x與w，最終的輸出結果爲0。證明者和驗證者知道電路輸出爲0，且公有輸入爲x的情況下，證明者需要證明自己知道祕密輸入 w。

算術電路➡R1CS

我們最終需要一個多項式，但算術電路不能直接轉化爲多項式，需要 R1CS 作爲二者間的媒介，故先將算術電路轉換爲 R1CS。

R1CS，全名爲 Rank-1 Constraints System（一階約束系統），是一種描述電路的語言，本質上是一種矩陣向量方程。具體來說，R1CS 是由三個向量 (a,b,c) 組成的序列，R1CS 的解是一個向量 s，其中 s 必須滿足方程：

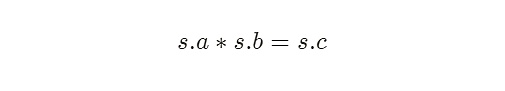
其中 . 代表內積運算。

此間具體的數學轉換可以參見 Vatalik：Quadratic Arithmetic Programs: from Zero to Hero

我們只需要知道，R1CS 的作用是對算術電路中的每個門的描述進行限定，使得每個門之間的向量滿足以上關系。

R1CS➡多項式

在得到 R1CS 這個媒介後，我們就可以將其等價轉換成多項式。

矩陣和多項式之間可以進行如下圖所示的等價轉換：

多項式

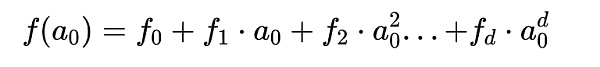
轉化爲矩陣

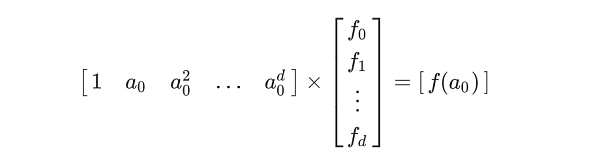
根據上述等價轉換的性質，對於滿足 R1CS 的矩陣，我們可以使用拉格朗日插值法，還原出多項式每一項系數，基於這個關系，我們可以將 R1CS 矩陣推導爲多項式關系，即：

注：A, B, C分別代表一個多項式

一個多項式對應我們想要證明的問題所對應的一個R1CS矩陣約束，通過以上轉化，我們可以知道，多項式之間滿足以上關系，就說明我們的R1CS矩陣是正確的，從而說明證明者在算術電路中的祕密輸入也是正確的。

到這我們的問題就簡化爲：驗證者隨機挑選一個數 x，讓證明者證明 A(x) * B(x)=C(x) 成立，如果成立，說明證明者的祕密輸入正確。

多項式之間的轉換

復雜的算術電路中，有成千上萬個門，我們需要對每個門驗證其是否滿足R1CS約束。換句話說，我們需要驗證數次 A(x) * B(x)=C(x) 等式成立，但是逐次單獨驗證的效率太低，如何能做到一次性驗證所有門的約束的正確性？

爲了方便理解，我們引入一個 P(x)，令 P(x) = A(x) * B(x) – C(x)

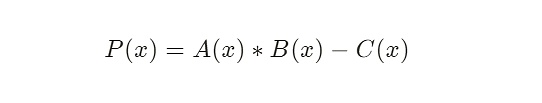
我們知道，任意的一個多項式只要它有解，就可以將它分解成线性多項式。故我們將 P(x) 拆分爲 F(x) 和 H(x)，即：

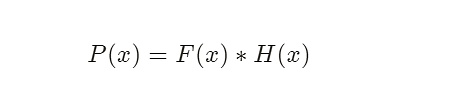
然後將 F(x) 公开，這就意味着存在一個 H(x) = P(x)/F(x) ，從而我們要驗證的多項式最終轉變爲 ：

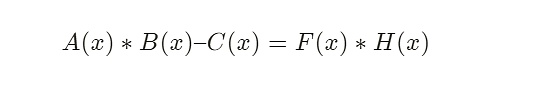
A(x) * B(x) – C(x)：包含多項式的系數，只有證明者知，即祕密輸入。

F(x) ：一個公开的多項式，驗證者和證明者皆知，即公开輸入。

H(x) ：證明者通過計算得知，驗證者不可知。

而最終要證明的問題爲：多項式等式 A(x) * B(x) – C(x) = F(x) * H(x)，在所有x上都成立。

現在只需要驗證一次多項式就可以驗證所有約束是否滿足矩陣關系。

到這裏我們就完成了將待證明的問題轉化成只需要驗證一次的多項式，實現了系統的簡潔性。

但是這個實現的簡潔性是讓驗證者的驗證時間縮短，那證明大小呢？

簡單來說，在證明協議中，使用的是 Merkle 樹的結構，這有效的降低了證明的大小。

整個轉換過程完成以後，自然而然的會產生兩個問題：

• 爲什么要轉換成多項式？

  因爲多項式實現了證明的簡潔性。零知識證明的問題就是驗證計算滿足多個約束的問題，而多項式可以一個點驗證多個約束。換句話說，驗證者本來要驗證 n 次才能確認的問題，現在只需要驗證一次就能極大概率地確認證明的正確性。

• 爲什么驗證多項式上的一個點，就能確定兩個多項式 A(x) * B(x) – C(x )= F(x) * H(x) 成立？

  這是由多項式的特性決定的，即：一個多項式在任意點的計算結果都可以看做是其唯一身份的表示。對於兩個多項式，它們只會在有限的點上相交。

對於上述的兩個 d 階多項式：A(x) * B(x) – C(x) 和 F(x) * H(x)，如果它們不相等，它們最多只會在d 個點上相交，也就是在 d 個點上的解相同。

完成了多項式的轉換，我們就要進入多項式證明階段。

證明多項式成立

爲了便於闡述，我們採用多項式 P(x) = F(x) * H(x)。

現在，證明者要證明的問題是：在所有 x 上，P(x) = F(x) * H(x)。

證明者和驗證者對以上多項式的驗證過程如下：

• 驗證者選擇隨機挑战點 x，假設 x = s；

• 證明者收到 s 後，計算 P(s) 和 H(s)，並把這兩個值給驗證者；

• 驗證者先計算 F(s)，再計算 F(s) * H(s)，並判斷 F(s) * H(s) = P(s) 是否成立，若成立則驗證通過。

但是我們仔細思考就會發現以上流程存在一些問題：

• 證明者能夠知道整個等式的信息，如果收到隨機點 s，他能計算出 F(s)，然後構造出一對假的 P(x) 和 H(x)，使得P(s) = F(s) * H(s) ，以此欺騙驗證者。

• 證明者不使用驗證者給出的 s 計算 F(s) 和 H(s)，而是用其他值計算，以此欺騙驗證者。

• 驗證者收到的值是由公共輸入和證明者的隱私輸入一起計算出來的，如果驗證者算力極大，可以破解證明者的隱私輸入。

針對上述問題，我們進行以下優化：

• 驗證者在選取了隨機點 s 後，對 s 進行同態加密，同態加密意味着加密後計算的解=計算後加密的解；在這種加密形式下，證明者能夠計算出解，但不能構造假的 P(x) 和 H(x)。

• 在驗證者選擇挑战點 s 時，再選取一個隨機參數 λ，額外生成一個 s 和 λ 之間的线性關系。驗證者把同態加密後的  s 和 λ 都發給證明者。待證明者將證明發回，驗證者除了驗證證明是否爲真，還需要驗證隨機參數λ 與 s 之間的關系。

• 針對驗證者可破解祕密輸入的問題，我們就可以引入 ZK。縱覽整個證明，我們可以發現在驗證過程中，證明者發給驗證者的只有計算出的多項式的值，驗證者可以通過值倒推出多項式的系數，即證明者的祕密輸入。爲了防止驗證者倒推，我們可以從 R1CS 推出多項式 A、B、C 的時候，多選取兩個隨機數並增加一組取值，這樣還原出來的多項式比原來的多項式多1階，從而讓驗證者無法從加密後的多項式中獲取原多項式的信息，以此實現 ZK。

優化以後我們發現證明系統依舊需要驗證者和證明者之間進行交互，如何才能實現非交互？

實現非交互

爲了實現非交互，SNARK 引入了可信設置（Setup）。

換句話說，在證明开始前，將原本屬於驗證者的選擇隨機挑战點的權力交給一個可信的第三方，第三方選擇了隨機參數 λ 後，將加密後的 λ 放在 R1CS 電路中，以此生成 CRS（Common Reference String，公共參考字串）。驗證方能從 CRS 中獲取屬於自己的 Sv，證明方能從 CRS 中獲取屬於自己的 Sp。

需要注意的是，λ 在生成 Sv 和 Sp 後，需要被銷毀，若 λ 被泄露，可能被用來通過虛假驗證僞造交易。

zk-SNARK 工作流程

在明白 SNARK 的構建流程後，基於我們構造的可生成證明的算術電路，zk-SNARK 的證明流程如下：

• Setup:(C circuit, λ)= (Sv, Sp)

  通過電路 C 和隨機參數 λ ，生成後續證明者和驗證者使用的隨機參數 Sv、Sp。

• Prove(Sp,x,w) = Π

  證明者通過隨機參數 Sp，公共輸入 x，祕密輸入 w，計算出證明 Π。

• Verify(Sv,x,Π) == (∃ w s.t. C(x,w))

  驗證者通過隨機參數 Sv，公共輸入 x 和證明 Π 來驗證是否存在 C（x,w）=0。同時，驗證證明是否是通過電路 C 計算得出。

到此，我們就完成了整個 zk-SNARK 的講解，下面來看看實際運用的案例。

案例：以 Scroll 的 zk Rollup 爲例

證明系統的作用是讓證明者說服驗證者相信一件事；

對於 zk 證明系統而言，是要讓驗證者相信由 zk 算法計算出的 Zero-Knowledge Proof（零知識證明）爲真。

我們以 Scroll 的 zk Rollup 爲例來說明 zk 證明系統的運行。

Rollup 是指鏈下計算，鏈上驗證。對 zk Rollup 而言，交易在鏈下執行後，證明者需要對交易執行後產生的新的狀態根生成 zk 證明，再將證明傳到 L1 Rollup 合約進行鏈上驗證。

需要注意的是，在 zk Rollup 中存在兩類區塊：

• L1 Rollup 區塊：提交到以太坊的區塊

• L2 區塊：用戶在 L2 上提交的交易打包而成的區塊

以下是 Scroll 的 zk Rollup 的工作流程：

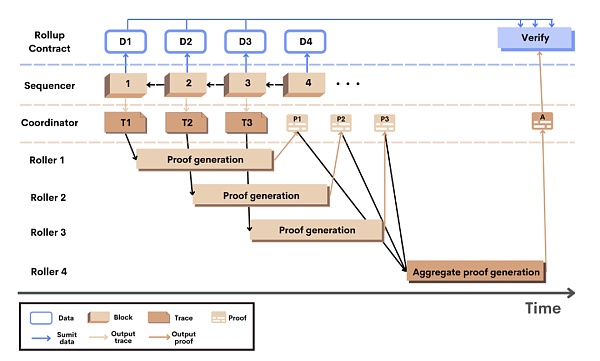
• 用戶在 L2 發起交易，Sequencer 檢索到交易，在鏈下執行交易並生成 L2 區塊和新的狀態根；同時將交易數據和新的狀態根提交給以太坊上的 Rollup 合約（提交交易數據是爲了實現數據可用性）；

• 當L2區塊生成時，Coordinator 會從 Sequencer 那收到該區塊的執行軌跡，然後將該軌跡隨機分配給任意一個 Roller；

• Roller 將接收到的執行軌跡轉換爲電路，且爲每個電路生成有效性證明，然後將該證明發回給 Coordinator；

• 每生成 k 個 L2塊，Coordinator 就會發送一個聚合任務給另一個 Roller，以將 k 個塊的證明聚合爲單個聚合證明；

• Coordinator 將單個聚合證明提交給 Rollup 合約，Rollup 合約結合之前提交的狀態根和交易數據一起驗證聚合證明，驗證通過則相應的區塊就被視爲在 Scroll 上最終確定。

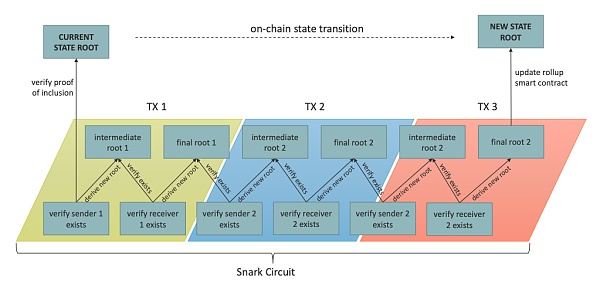
從以上流程可以看到，Roller 是該系統中的證明者，Rollup 合約是驗證者。Roller 對在鏈下執行的交易生成一個 zk 證明；Rollup 合約驗證該證明，若驗證通過，Rollup 合約就會直接採納提交的狀態根作爲自己新狀態根。

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。